ML-Normal Equation

What is normal equation, why shall we use it and how to use it?

What

之前我们提到使用梯度下降的方法来让损失函数达到最小值。这次，我们将不实用梯度下降的方法，我们将直接令Cost Function对$\theta$求导，使其为0来获得我们想要的最优的$\theta$。

Why

首先，我们解释一下为什么要使用Normal equation，使用梯度下降不是很爽吗？首先，我们来对比一下Gradient Descent 与 Normal equation。

显然，让当我们使用Gradient Descent时，我们需要人为的确定Learning rate、Iterations，然后有时候人为决定的值并不会有很高的效率（比如，我们对学习率与迭代次数到底要取多少根本不能准确的给出一个答案）。相对的，使用Normal Equation我们就避免了这个问题。但是我们可以看到，使用它也面临另外一个问题，那就是当我们的Features很多的时候，使用Normal Equation进行计算的效率会大打折扣，然而现实生活中的应用的Features可以是成千上万的，所以我们一般不会去用它。

How

怎么使用Normal Equation呢？就像我们一开始提到的，我们将直接让Cost Function对$\theta$求导，使其为0，求$\theta$即$\frac{\partial J(\theta)}{\partial\theta}=0$

例子🌰：以之前的Least squares为例

• $X : Matrix m by n+1 (include x_o which equals to 1)$
• $\vec y : Vector m by 1$
• $\theta: Vector n+1 by 1$

$J(\theta)=\frac{1}{2}\Sigma_{i=1}^{m}(h_\theta(x^i)-y^i)^2=\frac{1}{2}(X\theta-\vec y)^T(X\theta-\vec y)$

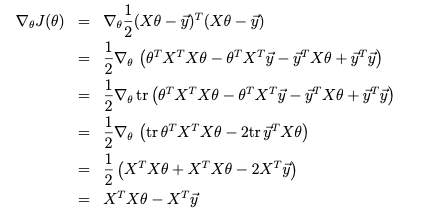
最后整理一下我们得到

$X^TX\theta=X^T\vec{y}$

$\theta=(X^TX)^{-1}X^T\vec y$

这东西就很好玩了，大家如果对线性代数有些了解，可能会想到投影矩阵$P=\frac{aa^T}{a^Ta}$

说的通俗一点就是可以通过投影矩阵把一个向量投影到X所在的空间，得到的就是最优解。

题外话：感兴趣的同学可以去回顾一下线性代数，说实话自己的线性代数也不大行，这里推荐MIT Strang的Linear algebra，可以在Youtube，B站，网易公开课找资料，个人建议不要开中文字幕，熬一熬适应了。当然，知乎上也有许多博主整理了自己的学习笔记，边看边学是不错的选择。

最后，使用Normal Equation求$\theta$时，可能会碰到$X^TX$不可逆的情况，这个时候可以用Pseudo Inverse。在Matlab, Octave, Numpy中可以使用pinv求解。

结束语：说实话这一节有点硬，实在不理解也不影响后续学习

本文由 Frank采用 署名 4.0 国际 (CC BY 4.0)许可

Machine Learning — 2021年4月20日