ML-Gradient Descent

什么是梯度下降？

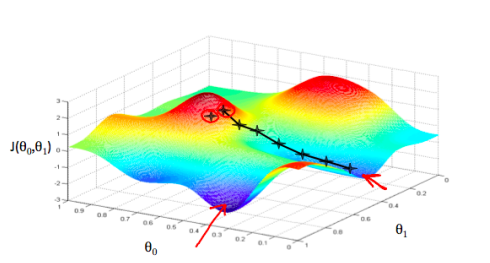
Gradient Descent，gradient是梯度，沿着梯度方向下降，就叫梯度下降。梯度即在某一点处切线的斜率（函数方向导数最大的方向，或函数变化最快的方向; $\frac{\partial f}{\partial l}=gradf.\vec l$, $\vec l$ 为单位向量）。如上图所示，求出某点处的导数( $\partial\theta_0$,$\partial\theta_1$ )，我们就得到了梯度的方向，就像下山一样，我们环顾四周，选一个最陡的方向往下走肯定是当前下山最快的方法。此处，我们还应该注意到，影响下山效率的，除了下山的方向之外，还有我们迈出的步长不是吗，那么我们应该迈出多大一步呢，此处便有了定义 $\alpha$，Learning rate，学习率。

知道了下山的方向和步长，那么怎么算到了山底，作为我们结束下山之旅的标志呢。显然的，当我们到达山底时，四周都是平坦的，我们的梯度为0，我们遍停下来，把该点算作自己的目的地（最优解）。

图中红色箭头指的两个点，分别是俩个局部最小点（局部最优解）。那为什么不是全局的最优解呢？因为，在有些情况下，我们的Cost Function可能是起起伏伏的，并不是Convex的,就导致了有许多点处的导数都为0的情况。根据起始点的不同，我们可能会到达不同的山底（局部最优解）。

梯度下降算法

Repeat until convergence {
$\theta_j:=\theta_j-{\alpha}\frac{\partial}{\partial\theta_j}J(\theta_0,\theta_1)$
}

这里要注意，更新迭代是同时的，既每次迭代的时候都要一起迭代 $\theta_0,\theta_1$

例子🌰

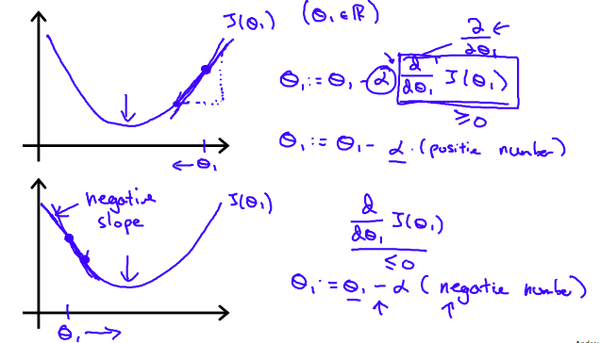
为了方便理解此处我们只考虑 $\theta_1$（不然会是等高线图，下面会提到）。从上方的图可以看出，当我们的起始点在右侧时，我们的梯度为正值，所以 $\theta_1-{\alpha}*\frac{\partial}{\partial\theta_1}J(\theta_1)$ 会使得 $\theta_1$ 逐渐向着局部最优解移动。同理的，我们可以推导一下起始点在左侧的情况。

接下来我们来讨论一下Learning rate:

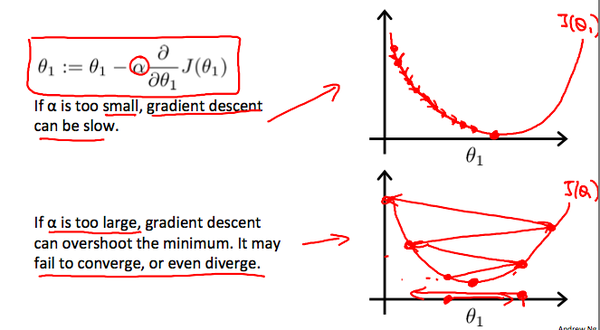
从上图可以明显的看出，当学习率小的时候，我们可以顺利的达到最优解，但是我们要迈出好多步，Andrew叫他Baby step。相反的，当我们的学习率取得较大的时候，可能会出现不能收敛的情况。当然，如果你取得 $\alpha$ 足够好，那么你讲以最快的速度达到山底（达到局部最优解）。一般的，我们通过不断尝试不同的learning rate，取最大的可以使得Cost Function收敛的值即可。

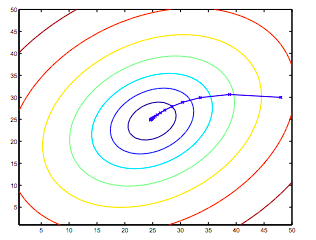
同时考虑 $\theta_0,\theta_1$ 的情况，沿梯度方向达到最优解。

结束语

目前考虑的是只有 $\theta_0,\theta_1$ 的情况，那么当特征多的时候又会是什么情况呢？我们能不能也通过简单的可视化来理解呢？

本文由 Frank采用 署名 4.0 国际 (CC BY 4.0)许可

Machine Learning — 2021年4月20日